If you are reading this now, you are probably one of those people who just hate algebra and completely flustered by it.
Guess what? It’s not as hard as it may first seem.
I’m sure when you were a kid in school, you did questions like these:
3 + ⬜ = 10 56 + ⬜ = 100 5 x ⬜ = 35 36 ➗ 4 = ⬜
⬜ + 14 = 20 100 – ⬜ = 37 ⬜ x 3 = 27 45 ➗ ⬜ = 5
Ring a bell?
If you are from an Asian family like me, then your parents bought you books filled with sums like these to do, as extra homework.
These types of questions are basic algebra questions, yet you can do these in your head.
For example, 100 – ⬜ = 37
All you have to do is 100 – 37 to find out the missing number. Again pretty obvious right?
Let’s take a look at the same question with more ‘algebraic’ notation:
100 – x = 37
All of a sudden, alarm bells might start ringing as this reminds you of the dread that is algebra.
Even though this question is easy to do in your head, here is how the working out would look like:
100 – x = 37
To get rid of x on the left side, we added x and because we added x on the left side we do it to the right side as well
100 – x + x = 37 + x
So far this is what it looks like
100 = 37 + x
To get rid of 37 on the right side, we subtracted 37 and because we subtracted 37 on the right side we do it to the left side as well
100 – 37 = 37 – 37 + x
So far this is what it looks like and now we can solve it
100 – 37 = x
63 = x same as saying
x = 63
Cool thing here is, we did all this in our head.
Schools and You
What schools aim for in trying to teach algebra is the step by step approach to working out the unknown(s) in a question.
As a student, you have to know the difference between the terms used and how they are applied in algebra. This is usually the part where many students get flustered and make mistakes that they normally would not.
Here is a list of the terms used and an example of each one:
| Rearrange or
make __ the subject of the formula |
Make y the subject or rearrange to make y the subject
5x = y + 7 y = 5x – 7 |
| Coefficient | This simply means the number that is attached to the variable like 5x. Here 5 would be the coefficient of x. |
| Substitute | When you have a value for a variable that you put into the equation.
Solve the equation, when y = 4. 7y + 3y = x Replace each y term with 4, always use brackets when doing this. 7(4) + 3(4) = x 28 + 12 = x x = 40 |
| Simplify | Collect all similar terms and then solve to simplify
4y + 2x – 3 + 3x + 8 Group the two terms with x in it. 2x + 3x + 4y + 8 – 3 now solve 5x + 4y + 5 |
| Factorise | Collect all the like terms and group them together by using brackets.
x2 + 2x = x(x + 2) [note it is meant to say x squared, same for below] Another example, factorise fully 9x2 – 6xy There is an x in both terms and both numbers have a factor of 3 3x(3x – 2y) |
| Common Factors | The is used when factorising, the term factors should ring a bell as it is also used when working with fractions. |
| Expand the
bracket or multiply out the bracket |
What this means is, show the same thing without using brackets
4(x +2) Multiply the 4 to each term inside the bracket 4x + 8 Another example, expand and simplify (x – 5)(x + 3) Multiply each term to each other x2 + 3x – 5x – 15 [note it is meant to say x squared, same for below] Then simplify = x2 – 2x – 15 |
| Equation | Always has an equals sign. Only works for certain values. For example, 5a + 10 = 25 |
| Formula | A calculation for a specific purpose and is always true no matter what value is put in. For example, area of a rectangle: length x width |
| Like terms | Get all the numbers and letters together, also used when simplifying.
2x + 3y + 4x + 7 Rearrange the terms with the same variables together and then likewise with individual numbers (also known as constants) 2x + 4x + 3y + 7 The step below would be simplifying = 6x + 3y + 7 |
| Difference of | Difference is found by subtracting one number from another. The difference between two squares means one squared term minus another squared term. (taken directly from BBC GCSE Bitesize) |
After familiarising yourself with all the terminology, you got to be able to apply it correctly time and time again. That is the part that most people just feel the ‘dread’ of algebra.
The solution to this, is to break down the problem and solve it one step at a time.
When your doing a difficult problem in school, slow down and realise where you made the mistake. If you are not sure where you made a mistake, just ask for help.
Your school is there to help you get a good grade and to be better at maths. It is in their best interest that you do well, so let them help you.
Is it true that some teachers are not that confident with maths? Yeah maybe, but the real question is, should that stop you from improving in maths?
The answer is no.
Here is why, there will always be people who are not as confident in maths as they should be even though they are capable of doing it. Letting non-confident people make you less confident is an easy cop out to not work smarter. Don’t let others put their insecurities on you, instead build your own confidence.
To avoid getting flustered you need to:
- Read – what the question is asking you to do
- Understand – the process needed
- Do – very clear line(s) of working out
Let’s take a walk through three exam questions.
Exam question #1
Question 12b, Maths non-calculator higher paper 1, 9th June 2014, Edexcel
This is only a 3 mark question.
If you don’t know what ‘make ___ the subject of the formula?’ means then you can’t even attempt the question.
To make ‘F’ the subject means instead of having ‘C = …’ make it so that it says ‘F = …’
Step 1: Multiply both sides by 9 to get rid of the fraction, so it looks like this
9C = 5(F – 32)
Step 2: Divide both side by 5. On the right side, the bracket is being multiplied by 5.
9C/5 = F – 32
Step 3: Add 32 to both sides
(9C/5) + 32 = F [Note, it’s pretty hard to write fractions on a document]
Or you can also write it like this
F = (9C/5) + 32
Three simple lines of working out gets the 3 marks.
The main stumbling block here is not reading the question carefully and therefore not understanding what is required.
Exam question #2
Solve the simultaneous equations* (4 marks)
3x + 4y = 5
2x – 3y = 9
*Question 15, Maths non-calculator higher paper 1, 6th November 2013, Edexcel
There are a number of ways solving this question. We are going to use the process of elimination to do this.
Step 1
Label the equations
3x + 4y = 5 [1]
2x – 3y = 9 [2]
Step 2
Work out how you can either get one x or one y. For this example do equation [1] – [2]. Note doing [2] – [1] gives the same thing.
[1] – [2]
Subtract all the like terms
3x – 2x = x
4y – -3y = 7y
5 – 9 = -4
All the bold terms will make the new equation
x + 7y = -4 [label this new equation, 3]
Step 3
Rearrange [3] to make x the subject
x = -7y – 4
Step 4
Now we have to substitute this x into either equation [1] or equation [2], to work out the value of y. Both will give the same answer.
Substitute x into [1], 3x + 4y = 5
3(-7y – 4) + 4y = 5
Step 5
Solve it, to find out what y equals
-21y – 12 + 4y = 5
-17y = 17
y = -1
Step 6
Substitute y into any of the three equations to solve x
Substitute y into [1]
3x + 4(-1) = 5
3x – 4 = 5
3x = 9
x = 3
Final answer x = 3, y = -1
Note, to double check just substitute these value into [1] or [2] to make sure it works.
Again very easy to shy away from this type of question, key here is to understand the process required to solve it and then working methodically.
Exam question #3
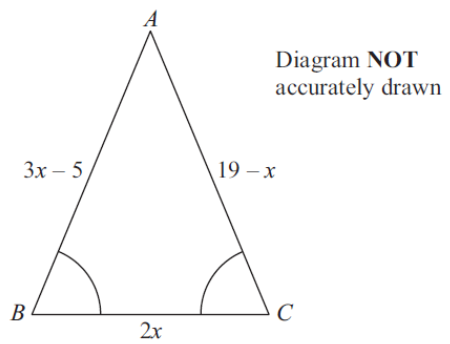
ABC is a triangle
Angle ABC = angle BCA.
The length of side AB is (3x – 5) cm.
The length of side AC is (19 – x) cm.
The length of side BC is 2x cm.
Work out the perimeter of the triangle.
Give your answer as a number of centimetres. [5 marks]
Question 8, Maths non-calculator higher paper 1, 6th November 2013, Edexcel
Here is a snazzy question, combines algebra with shapes. People usually will make mistakes either on the algebra or the shape aspect of the question.
Step 1
The question wants us to work out the perimeter of the triangle.
Must know that perimeter is the total distance around the shape.
The answer must be an exact number because it says, ‘Give your answer as a number of centimetres.’
Step 2
Work out what type of triangle it is to help solve what x is.
Hmmmm I wonder what triangle has two angles that are equal? Cue Gru from Despicable Me (2010).
Aha! An isosceles triangle, aaah but wait isosceles also have two equal sides.
This means that side AB and side AC are equal
3x – 5 = 19 – x
Step 3
Solve x
3x – 5 = 19 – x
4x = 24
x = 6
Step 4
Add all three sides together and substitute x in.
3x – 5 + 19 – x + 2x = perimeter
Substitute x in to solve or substitute x into each side and then solve
3(6) – 5 + 19 – (6) + 2(6) = 38
Or
side AB = 3(6) – 5
= 18 – 5
= 13
side AC = 19 – (6)
= 13
side BC = 2(6)
= 12
13 + 13 + 12 = 38
Final answer 38cm
This question combines all three of what you have to do:
- you got to read the question
- know and understand that the triangle has two equal sides (isosceles)
- solve x and find the answer
In each example, you noticed that the working out is very clear and easy to follow. Sounds simple but you would be surprised by how many sloppy mistakes happen by not having a clear method of working out.
By simply reading, understanding and applying what is needed to do the question, it is straightforward methodical work. When you start ‘getting it’ you will realise that the insecurity is baseless and you will gain confidence in your ability.
Stop hatin’ on algebra
Now you might say after reading all this, ‘I already know how to do all this stuff but I still hate algebra!’
I think one of the most annoying thing that people say about algebra being taught in school is that there is no relevance to it.
It is true that a lot of jobs don’t require you to be good at algebra or even maths.
Does that make it useless though? I don’t think so.
Here’s why:
The step by step approach required in algebra is also needed in other subjects for example science.
The flexibility of algebra within certain limits can enable great things to happen, take a look at technology. Brilliant example of this is how programming and coding has developed in the last few years.
Algebra helps to find unknowns by taking a methodical approach. You use this when finding out how to go somewhere new, ever used a map when you got lost?
To say it is completely useless is harsh, rather just say you don’t use it that way my heart doesn’t break.
Another reason why people hate algebra is because it is yet another thing to be tested on and stress about.
Look, exams and tests are stressful but so what? They are not going anywhere anytime soon in the UK, so might as well find a way to get better at them.
Algebra will definitely feature in maths exams. The point is not to memorise tons of formulas but rather to apply the right formula with the right method each time.
Hating on the topic doesn’t help you to improve in it which then becomes a downward spiral. Instead find out exactly what you are weak on, is it factorising or is it simultaneous equations etc.?
Pinpoint the problem and tackle it head on.
Remember, algebra is a topic that is fluid yet very structured. All you got to do is just take the mathematical approach and solve each problem methodically.
Got really stuck on an algebra problem? Put your name and email down and I can show how to tackle tricky questions. You don’t need to struggle by yourself anymore, I’ll make sure to make the complicated, straight forward for you.
[yikes-mailchimp form=”2″ submit=”Submit”]
Join me to discover that you can improve in maths. (Hint: improving in maths, means you can improve in other things too)

Put your name down to engage with me and I'll show you how to overcome your barriers in maths.
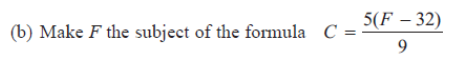

Thanks! Really helped I know many find Algreba tricky (like me) this post will really help.