Scared of Maths – It’s all in your head

Are you one of those people who feel intimidated by maths, feel like you can’t do it or that ‘maths is not for me’. If you are one of these people then continue reading.

A fear of a subject of study, in this case maths, can restrict the outcome of learning [1 and 2]. If your fear of maths is preventing your progression in maths then you should carefully pinpoint the fear.

Here are some of the most common fears listed below

1. Not understanding a process or formula
2. Not understanding how different aspects of maths are connected
3. Overwhelmed with how much to learn
4. Not getting the grade you want after putting in a lot of effort
5. Being seen as ‘dumb’ if you consistently ask for help
6. Not keeping up with the rest of the class/ peers
7. The expectations of your teacher(s) and family

More than likely if you are scared of maths than it could be a combination of some of the fears listed above.

Lack of understanding

Number one and two are problems to do with understanding concepts and applying them. Most students who don’t grasp concepts usually have weak or lack mental strategies.

For example,Taken from Edexcel GCSE – Paper 1 (Non Calculator) higher tier, 09 June 2014, paper ref. 1H

An easy 2 marks.

The process for adding or subtracting fractions is the denominator (bottom number) has got to be the same before you do anything.

To do a question like this, you would need to know how to find the Lowest Common Multiple for 5 and 3 and then be able to do the basic multiplication before the final subtraction.

Here is what the question looks like in the form of a diagram:

3/5      –    1/3

Method (for this section the diagram above will be referred to)

Due to the size of each of the portions in both shapes not being the same, it is not possible to do the subtraction straight away.

To try and do this subtraction we need to take away the shaded areas from each other:

This little bit that is left is the answer, trouble is we can’t represent it as a fraction accurately.

To solve this we have to make both shapes have the same amount of pieces to begin with

Note – yellow diagram has been rotated just to maintain the visual of the subtraction

9/15      –    5/15

Notice that even though there are more pieces in both shapes the size and the amount shaded is exactly the same as the original diagram above.

The two fractions denominators is 15, that is the Lowest Common Multiple (LCM) for 5 and 3. This means that a piece from the blue diagram is exactly the same size as the yellow one.

3/5 is equivalent to 9/15 and 1/3 is equivalent to 5/15 so the amount has not changed at all, only the numbers in the fractions themselves.

Now the subtraction can take place, 9 – 5 = 4

Note the denominator stays the same because there is a total of 15 pieces in both shapes.

After understanding the concepts behind subtracting fractions, you may not require to draw diagrams for every question. Once you fully understand the concepts, the steps to do this type of question are easy to follow:

• The two fractions denominators would be 15, that is the LCM for 5 and 3.
• Whatever is done to the denominator must be done to the numerator.
• Multiply the denominator to get to 15 and multiply the numerator by the same number.
• Now the subtraction for the numerators can be done and the denominators will stay the same.

Denominators and the Lowest Common Multiples of 3 and 5:

3, 6, 9, 12, 15

5, 10, 15

Numerators

For 3/5, We had to multiply 5 by 3 to get to 15 so we now have to multiply 3 by 3 which makes 9.

For 1/3, We had to multiply 3 by 5 to get to 15 so we now have to multiply 1 by 5 which makes 5.

Finally 9 – 5 = 4

The new denominator (15) stays the same.

Imagine a cake that had 15 pieces, there was 9 pieces left and now some people had 5 pieces. Obviously, there is only going to be 4 pieces left. The original amount of pieces to begin with did not change (15 pieces) hence why the denominator does not change when subtracting.

In the above example, it is clear that by not knowing the concepts and processes it is easy to get intimidated by a question like this. Similarly, it can be intimidating not knowing that different topics such as LCM, multiplication and subtraction are connected and required to do this one question.

Having deep conceptual understanding and following a step by step approach, using different aspects of maths, solves this question.

Psychological Barriers

Being overwhelmed by how much content to learn does not solve the issue of you still having to learn the content. With anything difficult or complicated that we learn to do, we always learn it by breaking the components down into more manageable parts. Once all the components of the task or concept has been broken down, the next step is to piece it together.

Take for example drawing nets for 3D shapes such as a cube or a cuboid. Not knowing which way the net will fold together can be off putting to even try the question.

What you need to know:

• the name of the shape and how it looks in its 3D form
• how the faces of the shape look like and the properties of those 2D shapes.
• how it pieces together.

Similarly, at GCSE level other topics can be broken down to a more understandable level and then pieced together once it has been fully understood [3a and 3b]. After understanding then space out the time practicing the topics. Practicing what you learn will help you to secure what you have already learnt.

Effort vs. Results

Simply put, just because you may study hard or revise a lot does not mean you should get a high grade. Why? Because when you are studying for the exam it is nothing like actually doing the exam for real. You can’t possibly simulate the real moment of exam pressure.

There are many cases of students who hardly study and get high grades and there are students who study a lot but fail on the day.

This boils down to how you study. Do you study efficiently and effectively?

Efficiently meaning how well you study. Effectively meaning what you study.

If when you study, you keep getting distracted or more anxious due to how close the exams are then it doesn’t matter how much you study because you are not at your optimal state.

You need to find a way where you can study at your peak, this includes self well being, environmental factors and timing.

Going over topics you already know should not be a priority. You should be going over the topics that you are most weak on or where you lose the most marks on.

The topics that you are strong in you should aim to iron out any sloppy mistakes and build up on the topics you are weak on.

The old but gold statement is true here, quality over quantity, work smarter to get higher results.

Studying a lot might not help if you are not able to retain or apply anything, but trying to rush your studying would definitely not help. The aim is to have focused study time of the most needed topics where you are mentally at your best whilst studying or revising.

Important questions to ask yourself:

1. When do I study/revise at my peak?
2. Is this the best use of my time going over ___ now?
3. Can I go over this topic ____ with somebody who can help me better? (e.g. teacher at school, tutor etc.)

Aim to optimise your learning and retention to get the most out of your time.

More effort ≠ higher grade. Instead, working smarter = higher grade.

Social Pressure

To not ask for help when you don’t understand something because you don’t want to seem ‘dumb’ doesn’t make any sense.

What is dumb is getting a lower grade than you should have because you were too afraid to ask for help. A lower grade that will stick with you for the rest of your life (unless you pay to do a retake).

In class, you may not always want to ask the teacher for help but you can always try look for the solution yourself or ask the person sitting next to you. You can even ask the teacher after class. If you are too afraid to ask for help publicly than that should not stop you from pursuing help privately.

The fear of being left behind is one which is very imposing if it is not dealt with properly. When you are in class, you want to stay at the same pace with the rest of the class but when you don’t understand something this could prevent your pace.

Again, due to not wanting to be seen as ‘dumb’ or not ‘up to scratch’, it might be tempting to just pretend and hide behind the progress of others hoping the teacher wouldn’t notice.

This makes no sense in the long run. Even if no one noticed that you are struggling, the exams you will take will expose that and you would not be able to blame anyone but yourself.

First of all, the idea of keeping up with others in general is not a good motto for life. Instead of excelling and leading others, you want to hide your potential to just ‘keep up’.

Was not expecting that…

Not meeting expectations from the people who mean a lot to you can be very disappointing. Maths is a very defined subject at GCSE so everything can be measured by either right or wrong. This then leads to tight definitions of grades and targets for students to get which can be motivating for some but devastating for many.

There two types of expectations that students deal with and the fears that pair them:

1. Others expect you to not do well, fear of fulfilling that prophecy.
2. Others expect you to do really well, fear of not achieving that grade and disappointing them.

When others are expecting less from you, this can negatively affect your approach to the ‘if I fail it’s not that big of a deal, I was expected to anyways’ mindset.

This negative stereotyping can make a person focus on not making mistakes instead of focusing on trying to maximise their answers.

To change this approach, DO NOT focus on the marks or grades you get. Instead focus on building and refining your methods and strategies and the grades will come with time.

Similarly, when others expect a lot from you, not meeting that expectation can add crippling pressure and be incredibly stressful.

This type of mindset can lead to what Carol Dweck calls ‘fixed mindset’ [4]. A fixed mindset essentially is someone who is afraid of challenges, failing and gives up easily.

When someone expects a lot from you, this can cap your growth. You would only try to meet their expectation instead of trying to surpass it. Another problem with this is that the focus is completely on the outcome and not the approach, deep learning is sacrificed for quick learning.

The outcome cannot be the only focus in maths because it can lead to rushing to answers without clear thought and reasoning.

Instead of having a fixed mindset develop what Dweck calls a ‘growth mindset’. Someone with a growth mindset keeps on trying on difficult problems, loves challenges and learns from mistakes made [4].

Don’t allow other people’s expectations of you to be scared of maths. The grades you get, after your exams, do not reflect you as a person, it is just a letter on a piece of paper that can be changed later on. Learn from any mistakes made and improve for next time.

Your confidence, effort and approach should enable you to improve your ability and end result. Overcome other’s expectations of you where they are left jaw dropped saying, ‘I was not expecting that!’

Use this cycle that my university teacher taught in class.

 

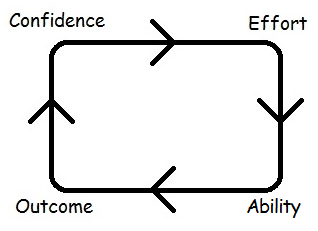
This cycle along with the steps discussed should help you in overcoming the fears you have in maths.

When you increase in one aspect of the cycle it builds momentum and allows you to develop and build in the other aspects of the cycle. This virtuous cycle should help you overcome your barriers to learning in maths and really any subject for that matter.

Reference

[1] Turner, S. (2013) Teaching Primary Mathematics. London: Sage Publications.

[2] Haylock, D. and Thangata, F. (2007) Key Concepts in Teaching Primary Mathematics. London: Sage Publications.

[3] Constructivist view of learning by Piaget and Zone of Proximal Development by Vygotsky

[a] Piaget, J. (1975) The Development of Thought. Oxford: Blackwell.

[b] Vygotsky, L. S. (1978) Mind in Society. Cambridge, MA: Harvard University Press.

[4] Dweck, C. S. (2006) Mindset the new psychology of success. New York: Ballantine Books.

Learn how to apply this cycle in more detail by putting your name and email down.

I will show you:

• how to build your confidence even on hard problems by giving you a mindset toolkit,
• how to channel your efforts in the right direction,
• what you need to keep track of to know if you are improving,
• how taking the right steps with time is going to improve your final results.

[yikes-mailchimp form=”2″ submit=”Submit”]